A Framework for Trusted Elections
We describe a simple but powerful framework for conducting trusted elections. We then show how the requirements of alternative voting methods, for example the ranked ballots required by STV PR, fit into the framework.
By a trusted election, we mean one in which voters can satisfy themselves that the outcome of the election is in fact the result of correctly counting all the ballots, and that each ballot correctly reflects the intent of the voter.
We accept that computers will be used to facilitate the election, given the number and size of elections in the United States. But we do not believe that computers can be trusted, in spite of (or perhaps because of) the fact that some of us have spent our professional careers working with them. Computer programmers and operators are humans, and thus both fallible and corruptible.
Nonetheless, computers are invaluable in keeping track of all the information associated with an election. Our task is to use them in such a way that we need not trust the computers in order to trust the election.
The Role of Secret Ballots
Ballots serve the important purpose as the record of voter intent. But the use of ballots, even without computerization, is not proof against errors or corruption, as is evident from corrupt paper-based elections around the world and through our own history. We can gain insight into the role of paper ballots, and the risks associated with their use, by examining even simpler and more transparent elections.
US Senate roll-call vote
We’ve probably all listened to a roll-call vote in the US Senate. The clerk reads the names of the senators, who respond with “yea” or “nay”. The responses are repeated and recorded. The counting rule is simple: a simple or super majority, depending on the question, with the added wrinkle that the Vice President, who serves as the President of the Senate, can vote to break a tie.
Trust is fairly easy in such an election. The voting is public, anyone watching or listening can keep their own tally, and each voter can double-check that their vote was correctly recorded.
College of Cardinals: electing a pope
The College of Cardinals, by contrast, elect a pope by a secret ballot, so the roll-call procedure can’t be used. Instead, each cardinal writes his vote on a slip of paper, folds it, and places it in a container, as three other cardinals, serving as “scrutineers”, watch. At end end of the voting, the scrutineers first count the total number of ballots; if they don’t match the number of voters, the ballots are burned and the process is repeated. The three scrutineers independently count the ballots, writing down the details. Three more cardinals, called “revisers”, double-check the count before the result is declared. (See Wikipedia’s papal conclave article for additional details and a rather fascinating history.)
Again, we can see that this would be a difficult system to attack. Ballot secrecy is not absolute, since the six scrutineers and revisers can see the handwriting on the ballots (but the ballots are burned, so no evidence of voter identity is retained). Ballot custody is transparent and in any case brief. The “audit”, by the revisers, is mandatory, complete, and immediate. Before the result is announced, the ballots will have been independently counted three times, and the counts independently checked three times.
Paper-ballot elections
A typical paper-ballot election introduces risks that are not present in the Senate roll-call vote or the papal conclave election.
In those two examples, it’s quite unlikely that an unauthorized vote will be cast—the voting takes place in person, face-to-face, with voters who are all well known to each other. Ballot custody is easy; there are no ballots in the Senate roll-call, and the papal-conclave ballots never leave the sight of the voters during their brief lifetime. Vote-counting is open and transparent, with no real opportunity for deceit.
But with typical paper-ballot elections, voters are not known to each other, and generally do not vote in a single physical location. Indeed, votes may be cast by mail. The vote-counting process can take several days, and with audits and recounts, the days extend into weeks. During the entire time (including as much as a month before election day during with voting by mail may be happening), the cast ballots must be kept secure from loss and tampering.
It’s not far-fetched to consider the possibility of corruption. Elections are often high-stakes affairs, and the US has a long history of ballot-box stuffing, dead or infant voters, and vote-buying. In general, though, we believe that that we know how to conduct a trustworthy election with paper ballots, and while the occasional exception is reported, we’re generally right.
Trust Overview
In order to trust an election, we must ensure that:
- The ballots are cast as intended; they represent the voters’ intentions.
- The ballot file is recorded as cast; it accurately represents the ballots as cast.
- The votes are counted as recorded; the counting software correctly implements the voting rule, correctly counts the correct ballots, and reports the correct outcome.
…where the “ballot file” is a computer file that represents all the ballots cast in the election.
We’ll elaborate a little on these three areas of trust.
- The ballots as cast represent the voters’ intentions. This requires voter-verifiable ballots, and it requires that we count what the voter verified. For example, if we have DRE (direct-recording electronic) with a paper trail, then the paper trail, not the DRE electronic output, is the authoritative reference.
- The ballot file accurately represents the ballots as cast. The file might mismatch for a number of reasons: corrupt or buggy DRE or scanning equipment, malicious or infected scanning software, etc. We will address this requirement with a risk-limiting audit, manually comparing the ballot file’s idea of the ballots to the authoritative paper ballot.
- The counting software accurately implements the voting rule, correctly counts the correct ballots and reports the correct outcome. This is difficult, perhaps impossible, to do by testing and inspection, though such testing and inspection needs to happen.As a practical matter, the only way to ensure trust here is by multiple independent counts, using multiple independent implementations of the rule. Ideally, this will be done in public: anybody with a counting program could take the ballot file and do a count, and verify that the reported result was in fact correct.
The key elements of the framework are 1) voter-verifiable paper ballots, 2) separating (in a risk-limiting audit) the verification of the ballot file against the ballots from the verification of the count itself, 3) cross-verification of the count by independent counting software, and 4) taking steps to guarantee ballot-file integrity.
Election Flow
The diagram below shows the general flow of an election conducted under these guidelines.
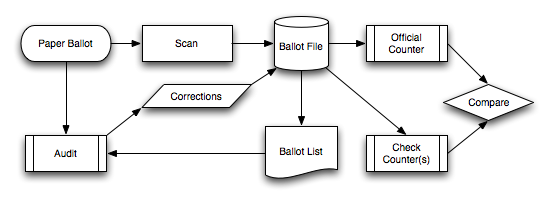
- Voters cast votes with paper ballots.
- Scan ballots and collect results in ballot file.
- Print ballot list from ballot file.
- Perform trial count to determine margin of election.
- Audit randomly selected ballots from ballot list against corresponding paper ballots.
- Append corrections to ballot file.
- Repeat steps 4–6 until risk of incorrect outcome is reduced to predetermined level.
- Count corrected ballot file with official counter.
- Count corrected ballot file is with independent check counters.
- Compare counts to verify counters.
The scanning function could also include the manual entry of ballot data.
DRE (direct-recording electronic) voting machines can be incorporated into the election flow as long as they include a voter-verifiable paper trail (VVPT) to serve as the authoritative reference for voter intent.
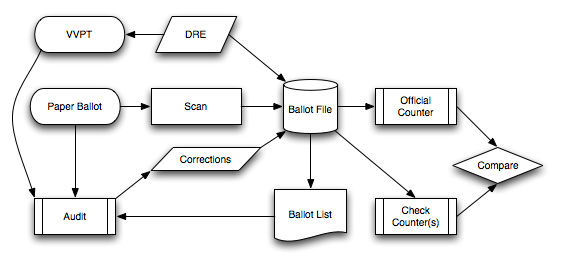
Accurate entry of ballot data (the creation of the ballot file) is desirable, in that mistakes at this stage will require time and labor to correct later on, so quality control is important. However, accuracy at this stage is not the source of our trust; the cost of mistakes is not trust, but rather a higher likelihood of requiring a full manual recount.
Election Flow Notes
- While the election flow diagrams show the ballot file as a single entity, in practice it need to be copied to other locations. To guarantee that each user of the ballot file (counters, auditors, backup) have identical files, a cryptographic message digest, or hash, is associated with the file. A message digest is a string of characters calculated as a function of the file whose value will be different whenever the file is different. Each user of the ballot file recalculates the message digest and compares it with the message digest published by the election official.
- Ballots in the ballot file are never altered. If the audit finds an erroneously recorded ballot, the correction is appended to the ballot file as a journal, and the corrections are published with their own message digest. Each user of the ballot file applies the corrections to the ballot data before using it. In this way, the ballot file and its subsequent corrections provide a permanent record of its history—an audit trail.
- The integrity of the election does not depend on trust of the voting machinery (scanners, DRE machines, etc). We still want them to be as reliable as possible, since errors make the audit process more laborious, but they are present only as a convenience; we rely on the voter-verified paper ballot or paper trail, not the recording machinery.
- Paper ballots, even in the complete absence of computers, cannot secure themselves. Voter trust depends on the paper ballots (or paper trail) being handled using existing best practices: secure storage, chain of custody, etc.
- Similarly, once the ballot file has been published, anyone can perform an independent count to verify that the official counter produced the correct result. We do not rely on any particular counter to be correct.
- The framework is compatible with any form of voting that results in an authoritative paper ballot or paper trail, as well as an electronic record, whether direct, scanned or manually entered. This flexibility is desirable for meeting accessibility requirements while at the same time accommodating vote by mail and various ballot formats.
- The framework is amenable to multiple-jurisdiction counts, where an election includes multiple districts with different voting equipment. In California, for example, each of its 58 counties is responsible for elections within the county, but elective districts can cross county lines.
Risk-Limiting Audits
What is a risk-limiting audit? ElectionAudits.org offers a good high-level definition: an audit with “a large, pre-determined minimum chance of leading to a full recount whenever a full recount would show a different outcome.”
The procedure for a risk-limiting audit is to compare original (or paper-trail) ballots, by hand, to the ballots-as-counted, and based on the detected error rate and the margin of election, determine the probability that a full hand recount would overturn the apparent election result. If that probability exceeds the pre-dermined minimum, the sample size is increased until the probability is sufficiently low, or until a full manual recount has been performed.
The logic is straightforward: we either prove to ourselves that the statistical likelihood of a manual count overturning the original outcome of an election is negligible (which may require increasing our sample size if we detect errors), or we proceed to a manual count.
In general, closer margins of election require larger samples, and higher detected error rates require larger samples yet. Errors are detected more efficiently as the batch size of the ballots randomly selected for manual checking grows smaller. The practice of recounting a random sample of entire precincts is inefficient compared to sampling individual ballots, where by “inefficient” we mean that a substantially larger number of ballots must be checked to arrive at some level of confidence about the error rate.
Technology Factors
While our framework does not depend for its trust on the trustworthiness of any particular computer, it does employ certain technological solutions to trust problems. These solutions are straightforward, and the nature of their trust is readily apparent to non-technical observers.
Message digests
The message digest is a bit of cryptography that converts a string of data (in our case the ballot file) into a shorter string of characters. Here’s a simple example of a message digest; you can see that a small change in the data results in a large change in the digest.
| text | message digest |
|---|---|
| “Mary had a little lamb.” | e1656e417993e7977d222cb4564c29b6 |
| “Mary had a little lamp.” | eaaa9870a3445e029cc77854c054e24a |
| “Mary has a little lamb.” | 59b6edb515effff3d5c9f3c4c4fe794f |
| “Mary has a little lamp.” | b6a6d233e8ca3f1e4b3f25a9bf0addbc |
When the message digests of two files match, we can be quite certain that the files are identical. One needn’t understand the bits and bytes of the cryptography involved to understand the general principle, and how it’s used in the framework. When we obtain a copy of the ballot file for counting or auditing, we calculate the message digest of the copy and compare it to the published message digest of the original ballot file to ensure that we have an identical copy of the file.
(The example uses a simple message digest called MD5. In practice, we would use a longer and more robust message digest, such as SHA-2 or SHA-3.)
Risk-limiting audits
The principle of a risk-limiting audit is simple: we randomly check the integrity of individual ballots in the ballot file against their authoritative paper version. The technology we’re trusting here is based in the branch of mathematics called statistics. We employ formulas that tell us, based on the details of a particular election, just how many ballots we have to verify in order to be confident that the result of counting the ballot file would be identical to that of manually counting all the paper ballots.
The mathematics can be subtle, but the principle is straightforward, as are the actual calculations. And by performing the calculations transparently, they can be subjected to the scrutiny of independent (and skeptical) statisticians.
Election-counting software
Finally, we rely on vote-counting software. The logic for counting an election ranges from the trivial (add up the votes for each candidate in a plurality election) to the slightly more complicated count of an instant-runoff (IRV) election, to the rather subtle algorithms of Meek’s method of STV PR.
Our trust mechanism, though, is simple and transparent in all cases: anyone can take the ballot file, and use their own counting software to check the result of the official counting software. As long as we know that independent, skeptical third parties are counting the election in tandem with the official count, we can be quite confident that the count is being performed correctly.
The independent counters might be opposing political parties, good-government groups like the League of Women Voters, or any interested group that wants to try their hand at election counting.
STV and Trusted Elections
The election framework we’ve been describing is congenial to STV elections (including single-seat IRV elections). This is largely because two of its characteristics (separating the creation and verification of the ballot file from counting the resulting file, and the use of a risk-limiting audit with single-ballot sampling) make the process largely independent of the form of the ballot and the nature of the count.
STV and Risk-Limiting Audits
Auditing STV elections presents challenges not present in auditing conventional plurality-winner elections. First, it’s not practical (or meaningful) to count a subset of an STV election (recounting a sample precinct, for example). Second, STV requires a broader definition of “margin of election”, because the STV counting process requires a series of intermediate decisions with their own margins (such as defeating low-vote candidates) that potentially affect the outcome of the count.
Sampling individual ballots (as opposed to larger batches) is desirable for another reason when auditing an STV (including IRV) election. Not only is the sample size smaller, but it’s practical to check the entire ballot (all rankings) at once. The manual ballot check procedure is separated from the count itself.
Coincidentally, single-ballot sampling is also desirable when performing risk-limiting audits of simple majority elections, because the number of ballots that must be manually checked to arrive at a given confidence level is much smaller than the number required when sampling by batch. This table, from Philip Stark, illustrates the advantage of randomly sampling individual ballots instead of larger batches when performing an audit.
| misinterpreted ballots by precinct |
random precinct of 500 |
10 random batches of 50 |
simple random sample of 500 |
|---|---|---|---|
| 10 in every precinct | 100% | 100% | 99.996% |
| 10 in 98 precincts, 20 in 1 precinct | 99% | ≈100% | 99.996% |
| 20 in 50 precincts | 50% | 99.9% | 99.996% |
| 250 in 4 precincts | 4% | 33.6% | 99.996% |
| 500 in 2 precincts | 2% | 18.4% | 99.996% |
STV (including IRV) introduces another factor into audits: the margin of election in an STV election is not simply the winning margin at the last stage of the count, but includes all the intermediate decisions that lead to the final result, such as the decision to defeat low-vote-count candidates in cases where defeating a different candidate could lead to a different election outcome. It’s worth noting that, for auditing purposes, nothing is lost by using a lower bound of the margin of election instead of an exact value, except that the sample size may be somewhat larger.
STV and count-checking
Counting an STV election ballot file is more complicated than counting a simple plurality election, and the preferred STV counting rules are generally counted by computer. Separating ballot-file creation and auditing from the count allows us to be independent of any particular computer count, and to allow, even encourage, the use of multiple independent counters. This adds to the transparency of the election, and provides a straightforward means to achieve trust in the election outcome without trusting the official counting software.
It’s worth noting that the use of open-source election software is not in itself an answer to the computer-trust program. Open-source software is as subject to bugs as commercial software is. Perhaps more significant, it’s effectively impossible to know for certain that the software running in a computer is in fact identical to the software that has been examined and certified. Multiple independent counters sidesteps this problem.
Thanks to the Prêt à Voter group, from whom we’ve borrowed some election-integrity language.
